« home

One Point

Tags

physicsquantum field theoryrenormalization

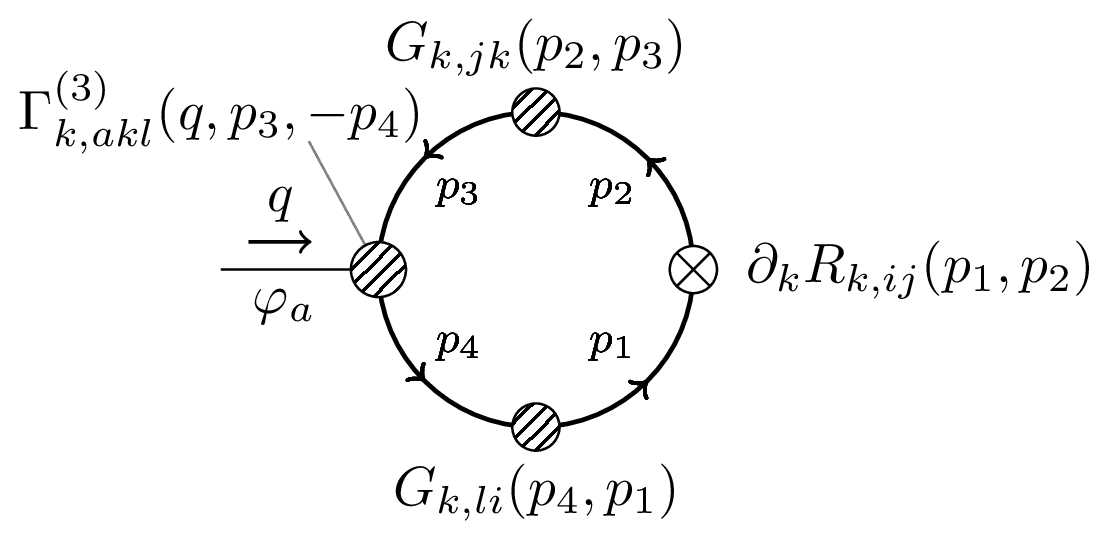
This Feynman diagram corresponds to the integrand in this expression for ∂tΓk,a(1)(q)=−12∑i,jk,lN∫p1,p2p3′,p4′∂tRk,ij(p1,p2)Γk,jk(2)(p2,p3)+Rk,jk(p2,p3) Γk,akl(3)(q,p3,p4)Γk,li(2)(p4,p1)+Rk,li(p4,p1).\displaystyle \partial_t \Gamma_{k,a}^{(1)}(q) = -\frac{1}{2} \sum_{\substack{i,j\\k,l}}^N \int_{\substack{p_1,p_2\\p_3^\prime,p_4^\prime}} \frac{\partial_t R_{k,ij}(p_1,p_2)}{\Gamma_{k,jk}^{(2)}(p_2,p_3) + R_{k,jk}(p_2,p_3)} \, \frac{\Gamma_{k,akl}^{(3)}(q,p_3,p_4)}{\Gamma_{k,li}^{(2)}(p_4,p_1) + R_{k,li}(p_4,p_1)}.


One Point

  Edit

Overleaf Logo Open in Overleaf

  Download

PNG PNG (HD) PDF SVG TeX

  Code

one-point.tex (39 lines)

\documentclass[tikz]{standalone}

\usetikzlibrary{patterns,decorations.markings}

\tikzset{
    cross/.style={fill=white,path picture={\draw[black]
        (path picture bounding box.south east) -- (path picture bounding box.north west)
        (path picture bounding box.south west) -- (path picture bounding box.north east);}},
    dressed/.style={fill=white,postaction={pattern=north east lines}},
    momentum/.style={->,semithick,yshift=5pt,shorten >=5pt,shorten <=5pt},
    loop/.style 2 args={thick,decoration={markings,mark=at position {#1} with {\arrow{>},\node[anchor=\pgfdecoratedangle-90,font=\footnotesize] {$p_{#2}$};}},postaction={decorate}},
    label/.style={thin,gray,shorten <=-1.5ex}
}

\def\lrad{1}
\def\mrad{0.175*\lrad}
\def\srad{0.15*\lrad}

\begin{document}
\begin{tikzpicture}[pin edge={shorten <=5*\lrad}]

  % Loop
  \draw[loop/.list={{0.125}{2},{0.125*3}{3},{0.125*5}{4},{0.125*7}{1}}] (0,0) circle (\lrad);
  \draw[cross] (\lrad,0) circle (\srad) node[right=6pt] {$\partial_k R_{k,ij}(p_1,p_2)$};
  \draw[dressed] (0,\lrad) circle (\srad) node[above=3pt] {$G_{k,jk}(p_2,p_3)$};
  \draw[dressed] (0,-\lrad) circle (\srad) node[below=3pt] {$G_{k,li}(p_4,p_1)$};

  % External line
  \draw (-2*\lrad,0) -- (-\lrad,0) node[pos=0.4,below] {$\varphi_a$};
  \draw[momentum] (-2*\lrad,0) -- (-1.25*\lrad,0) node[midway,above] {$q$};

  % Vertex
  \node (Gkakl) at (-2*\lrad,\lrad) {$\Gamma_{k,akl}^{(3)}(q,p_3,-p_4)$};
  \draw[label] (Gkakl.-30) -- (-\lrad,0);
  \draw[dressed] (-\lrad,0) circle (\mrad);

\end{tikzpicture}
\end{document}