Normalizing Flow
Tags
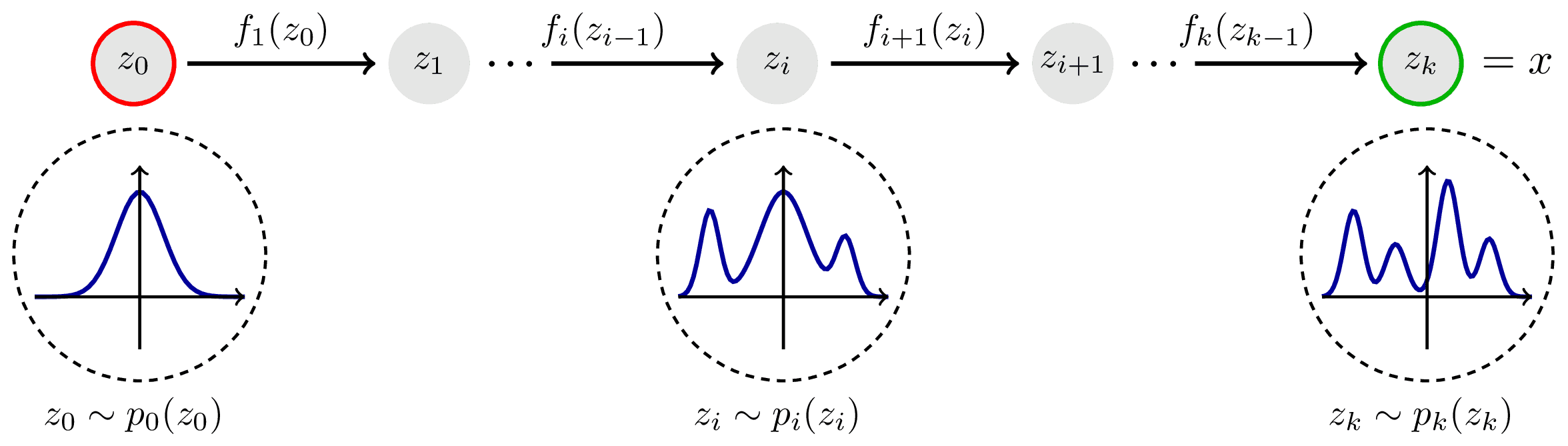
A chain of bijections constituting a normalizing flow which step by step transforms a simple distribution into a complex one . The bijections are trained to fit to some target distribution . Inspired by Lilian Weng.
Edit
Download
Code
normalizing-flow.tex (39 lines)
\documentclass[tikz]{standalone}
\usetikzlibrary{positioning}
\newcommand{\distro}[4][40]{
\begin{tikzpicture}[thick]
\draw[dashed, dash pattern={on 2.3 off 2}] (0, .4) circle (12mm);
\draw[blue!60!black, very thick] plot[variable=\t, domain=-1:1, samples=#1] ({\t}, {#2 * exp(-10*(\t)^2) + #3 * exp(-60*(\t-0.6)^2 - \t) + #3 * exp(-60*(\t+0.7)^2 - 0.2) + #4 * 0.5 * exp(-50*(\t+0.3)^2) + #4 * exp(-50*(\t-0.2)^2 + 0.1)});
\draw[solid, ->] (-1, 0)--(1, 0);
\draw[solid, ->] (0, -0.5)--(0, 1.25);
\end{tikzpicture}
}
\begin{document}
\begin{tikzpicture}[
node distance=2, very thick,
flow/.style={shorten >=3, shorten <=3, ->},
znode/.style={circle, fill=black!10, minimum size=22, inner sep=0},
]
\node[znode, draw=red] (z0) {$z_0$};
\node[znode, right=of z0] (z1) {$z_1$};
\draw[flow] (z0) -- node[above, midway] {$f_1(z_0)$} (z1);
\node[znode, right=2.5 of z1] (zi) {$z_i$};
\node[znode, right=of zi] (zip1) {$z_{i+1}$};
\draw[flow] (zi) -- node[above, midway] {$f_{i+1}(z_i)$} (zip1);
\draw[flow, shorten <=5ex] (z1) -- node[pos=0.16, inner sep=1] {\textbf\dots} node[above, midway] {$f_i(z_{i-1})$} (zi);
\node[znode, draw=green!70!black, right=2.5 of zip1] (zk) {$z_k$};
\draw[flow, shorten <=5ex] (zip1) -- node[pos=0.16, inner sep=1] {\textbf\dots} node[above, midway] {$f_k(z_{k-1})$} (zk);
\node[right=0 of zk, scale=1.2] {$= x$};
\node[outer sep=0, inner sep=0, below=0.2 of z0, label={below:$z_0 \sim p_0(z_0)$}] (f0) {\distro{1}{0}{0}};
\node[outer sep=0, inner sep=0, below=0.2 of zi, label={below:$z_i \sim p_i(z_i)$}] (fi) {\distro[70]{1}{1}{0}};
\node[outer sep=0, inner sep=0, below=0.2 of zk, label={below:$z_k \sim p_k(z_k)$}] (fk) {\distro[90]{0}{1}{1}};
\end{tikzpicture}
\end{document}