NF Coupling Layer
Tags
Simple 2d example illustrating the role of the Jacobian determinant in the change of variables formula. Inspired by Ari Seff in https://youtu.be/i7LjDvsLWCg?t=250.
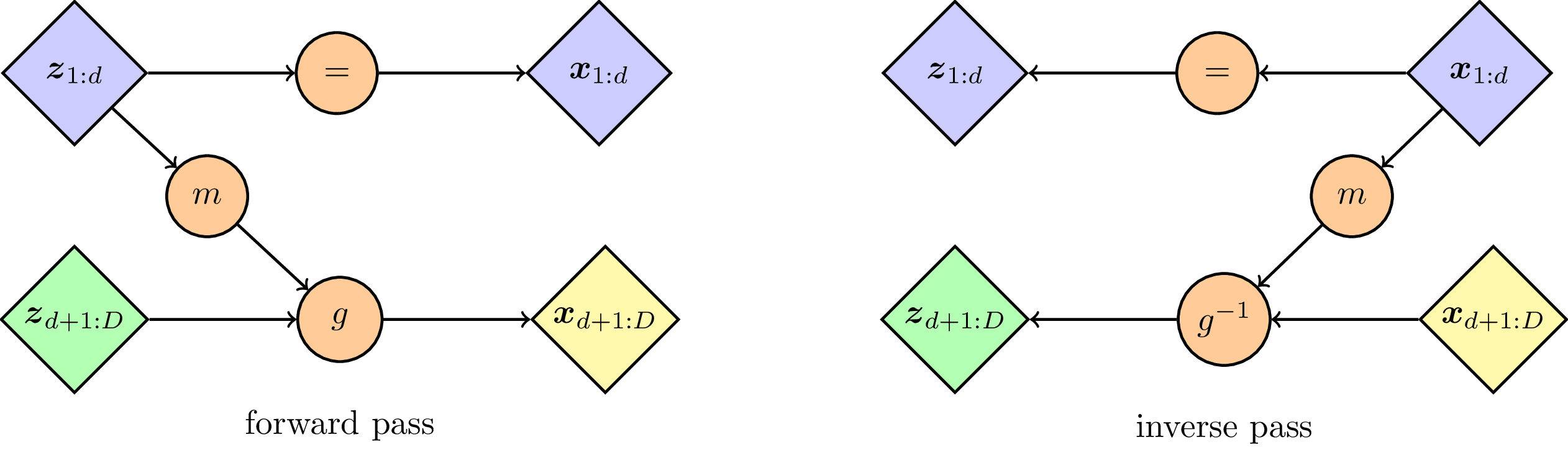
Edit
Download
Code
nf-coupling-layer.tex (50 lines)
\documentclass[tikz]{standalone}
\usepackage{mathtools}
\usetikzlibrary{calc,positioning,shapes.geometric}
\renewcommand\vec[1]{\boldsymbol{#1}}
\begin{document}
\begin{tikzpicture}[
thick, node distance=15mm,
set/.style={draw, diamond, text width=8mm, align=center},
op/.style={draw, circle, text width=5mm, align=center, fill=orange!40},
]
\node[set, fill=blue!20] (z1) {$\vec z_{1:d}$};
\node[op, right=of z1] (eq) {\raisebox{-1ex}=};
\node[set, right=of eq, fill=blue!20] (x1) {$\vec x_{1:d}$};
\draw[->] (z1) edge (eq) (eq) edge (x1);
\node[set, below=1 of z1, fill=green!30] (z2) {$\mathclap{\vec z_{d+1:D}}$};
\node[op, right=of z2] (g) {$g$};
\node[below=1em of g] (forward) {forward pass};
\node[set, right=of g, fill=yellow!40] (x2) {$\mathclap{\vec x_{d+1:D}}$};
\draw[->] (z2) edge (g) (g) edge (x2);
\node[op] (m) at ($(z1)!0.5!(g)$) {$m$};
\draw[->] (z1) edge (m) (m) edge (g);
\begin{scope}[xshift=9cm]
\node[set, fill=blue!20] (z1) {$\vec z_{1:d}$};
\node[op, right=of z1] (eq) {\raisebox{-1ex}=};
\node[set, right=of eq, fill=blue!20] (x1) {$\vec x_{1:d}$};
\draw[<-] (z1) edge (eq) (eq) edge (x1);
\node[set, below=1 of z1, fill=green!30] (z2) {$\mathclap{\vec z_{d+1:D}}$};
\node[op, right=of z2] (g) {$\mathclap{g^{-1}}$};
\node[below=1em of g] (inverse) {inverse pass};
\node[set, right=of g, fill=yellow!40] (x2) {$\mathclap{\vec x_{d+1:D}}$};
\draw[<-] (z2) edge (g) (g) edge (x2);
\node[op] (m) at ($(x1)!0.5!(g)$) {$m$};
\draw[->] (x1) edge (m) (m) edge (g);
\end{scope}
\end{tikzpicture}
\end{document}