Matsubara Contour 1
Tags
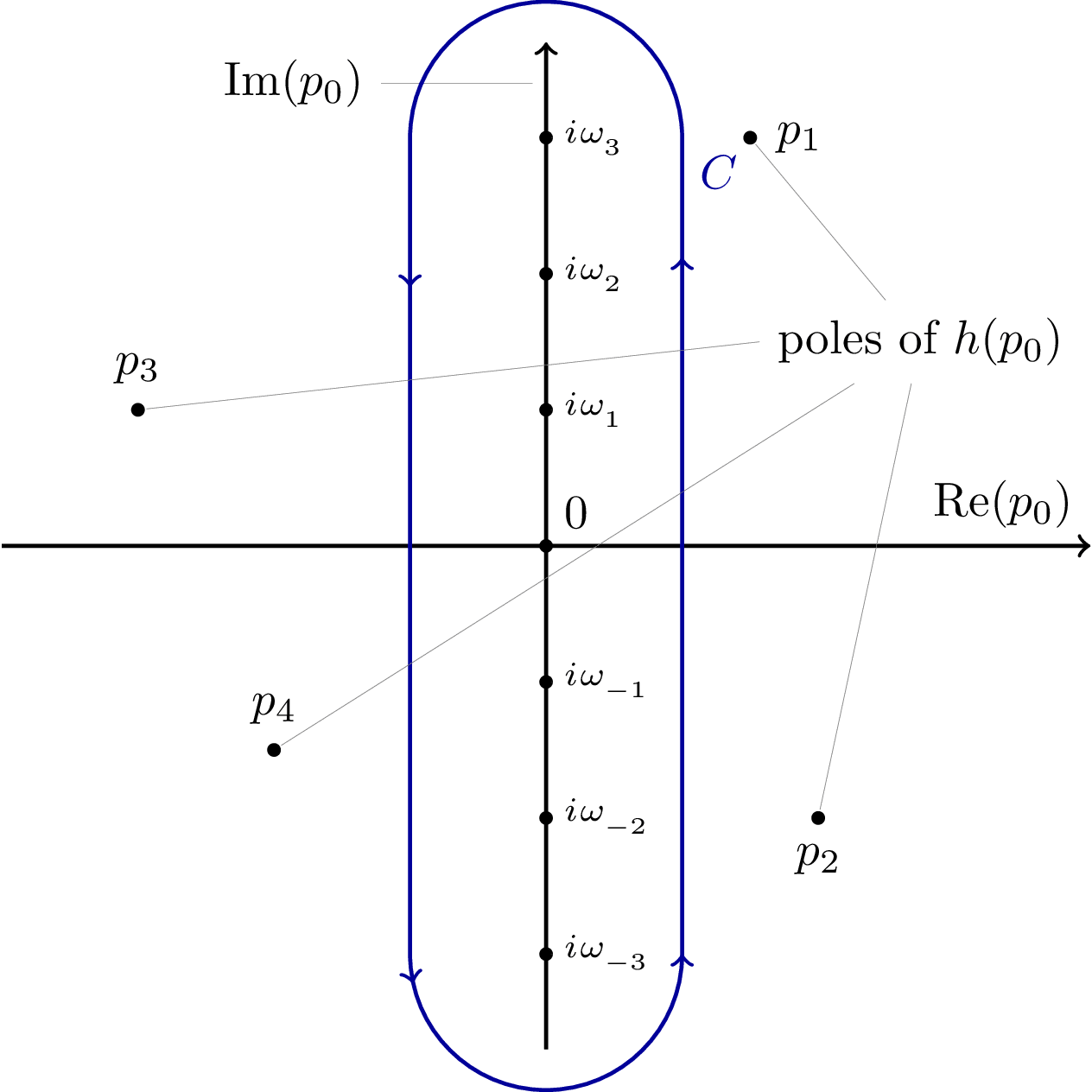
Complex contour plot illustrating a Matsubara summation. Used in thermal quantum field theory to compute Feynman diagrams at non-zero temperature. surrounds the imaginary -axis counterclockwise but excludes poles of .
Edit
Download
Code
matsubara-contour-1.tex (47 lines)
\documentclass[tikz]{standalone}
\usepackage{mathtools}
\let\Im\relax
\DeclareMathOperator{\Im}{Im}
\let\Re\relax
\DeclareMathOperator{\Re}{Re}
\usetikzlibrary{decorations.markings,positioning}
\providecommand{\poles}{
\node (poles) at (2.75,1.5) {poles of $h(p_0)$};
\draw[fill]
(1.5,3) coordinate [circle,fill,inner sep=1pt,label=right:$p_1$] (p1)
(2,-2) coordinate [circle,fill,inner sep=1pt,label=below:$p_2$] (p2)
(-3,1) coordinate [circle,fill,inner sep=1pt,label=above:$p_3$] (p3)
(-2,-1.5) coordinate [circle,fill,inner sep=1pt,label=above:$p_4$] (p4);
\draw[ultra thin,gray] (poles) -- (p1) (poles) -- (p2) (poles.west) -- (p3) (poles) -- (p4);
}
\def\xr{3}
\def\yr{3}
\begin{document}
\begin{tikzpicture}[thick]
% Axes
\draw [->] (-\xr-1,0) -- (\xr+1,0) node [above left] {$\Re(p_0)$};
\draw [->] (0,-\yr-0.7) -- (0,\yr+0.7) coordinate [below left = 0.3 and 0.1] (y-axis);
\node (y-label) at ([xshift=-50]y-axis) {$\Im(p_0)$};
\draw[ultra thin,gray] (y-axis) -- (y-label);
% Matsubara frequencies
\foreach \n in {-\yr,...,-1,1,2,...,\yr}{%
\draw[fill] (0,\n) circle (1pt) node [right,font=\scriptsize] {$i \mkern1mu \omega_{_{\n}}$};}
\draw[fill] (0,0) circle (1pt) node [above right] {0};
% Contour line
\draw[blue!60!black,decoration={markings,mark=between positions 0 and 1 step 0.28 with \arrow{>}},postaction={decorate}] (1,-\yr) -- (1,\yr) node [below right] {$C$} arc (0:180:1) (-1,\yr) -- (-1,-\yr) arc (180:360:1);
% Poles of h(p_0)
\poles
\end{tikzpicture}
\end{document}