Matsubara Contour 2
Tags
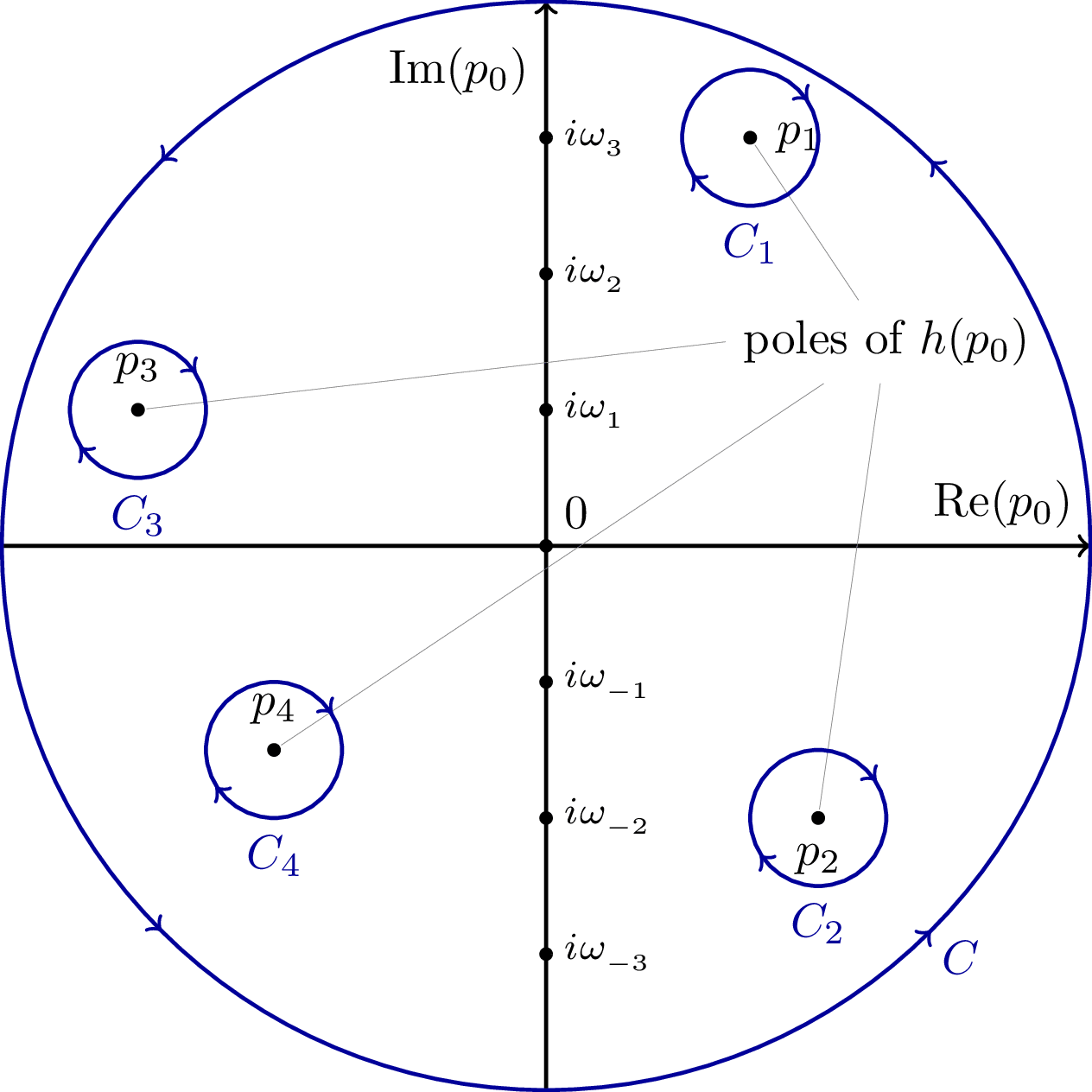
Deformation of contour in Matsubara contour 1 into a circle followed by taking the radius to infinity. This will enclose the poles of scattered throughout the complex plane. Their contribution is removed again by enclosing them in clockwise contours.
Edit
Download
Code
matsubara-contour-2.tex (55 lines)
\documentclass[tikz]{standalone}
\usepackage{mathtools}
\let\Im\relax
\DeclareMathOperator{\Im}{Im}
\let\Re\relax
\DeclareMathOperator{\Re}{Re}
\usetikzlibrary{decorations.markings,positioning}
\providecommand{\poles}{
\node (poles) at (2.5,1.5) {poles of $h(p_0)$};
\draw[fill]
(1.5,3) coordinate [circle,fill,inner sep=1pt,label=right:$p_1$] (p1)
(2,-2) coordinate [circle,fill,inner sep=1pt,label=below:$p_2$] (p2)
(-3,1) coordinate [circle,fill,inner sep=1pt,label=above:$p_3$] (p3)
(-2,-1.5) coordinate [circle,fill,inner sep=1pt,label=above:$p_4$] (p4);
\draw[ultra thin,gray] (poles) -- (p1) (poles) -- (p2) (poles.west) -- (p3) (poles) -- (p4);
}
\providecommand{\polecontours}{
\draw[blue!60!black,decoration={markings,mark=between positions 0.03 and 1.03 step 0.125
with \arrow{<}},postaction={decorate}] (p1) circle (0.5) node [below=0.5] {$C_1$} (p2)
circle (0.5) node [below=0.5] {$C_2$} (p3) circle (0.5) node [below=0.5] {$C_3$} (p4)
circle (0.5) node [below=0.5] {$C_4$};
}
\begin{document}
\begin{tikzpicture}[thick]
\def\xr{3} \def\yr{3}
% Axes
\draw [->] (-\xr-1,0) -- (\xr+1,0) node [above left] {$\Re(p_0)$};
\draw [->] (0,-\yr-1) -- (0,\yr+1) node [below left=0.2 and 0] {$\Im(p_0)$};
% Matsubara frequencies
\foreach \n in {-\yr,...,-1,1,2,...,\yr}{%
\draw[fill] (0,\n) circle (1pt) node [right,font=\footnotesize] {$i \mkern1mu \omega_{_{\n}}$};}
\draw[fill] (0,0) circle (1pt) node [above right] {0};
% Contour line
\draw[blue!60!black,decoration={markings,mark=between positions 0.125 and 0.875 step 0.25 with \arrow{>}},
postaction={decorate}] circle (\yr+1) node [below right=0.925*\xr and 0.925*\yr] {$C$};
% Poles
\poles
% Pole contours
\polecontours
\end{tikzpicture}
\end{document}