« home

Kohn Sham Cycle

Tags

physicsquantum mechanicsdensity functional theory

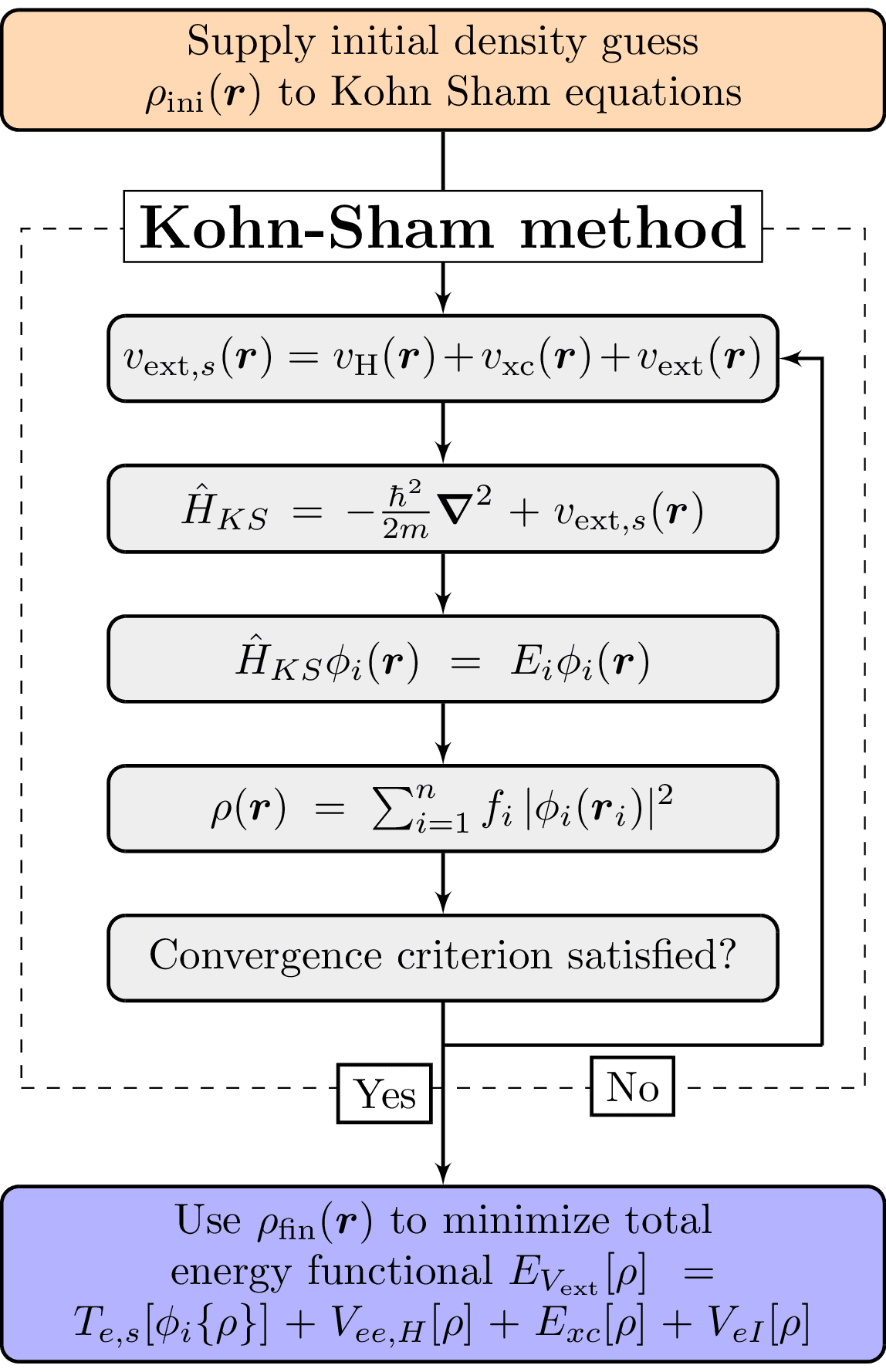
This diagram illustrates the Kohn-Sham cycle in Density Functional Theory (DFT), a computational quantum mechanical modeling method. The process starts with an initial guess for the electron density, which is used to calculate the effective potential. This potential is then used in the Kohn-Sham Hamiltonian, which is solved to obtain the wavefunctions. These wavefunctions are used to compute a new electron density. If convergence criteria are met, the final electron density is used to calculate the total energy functional. If not, the new electron density is used for the next iteration of the cycle.


Kohn Sham Cycle

  Edit

Overleaf Logo Open in Overleaf

  Download

PNG PNG (HD) PDF SVG TeX

  Code

kohn-sham-cycle.tex (43 lines)

\documentclass[tikz,svgnames,border={0 2}]{standalone}

\usepackage{mathtools}

\usetikzlibrary{positioning,arrows,fit}

\renewcommand\vec[1]{\boldsymbol{#1}}

\begin{document}
\begin{tikzpicture}[
    box/.style={rectangle,draw,fill=DarkGray!20,node distance=1cm,text width=15em,text centered,rounded corners,minimum height=2em,thick},
    arrow/.style={draw,-latex',thick},
  ]

  \node [box] (potential) {$v_{\text{ext},s}(\vec r)=v_\text{H}(\vec r) + v_\text{xc}(\vec r) + v_\text{ext}(\vec r)$};
  \node [box,below=0.5 of potential] (hamiltonian) {$\hat{H}_{KS}=-\frac{\hbar^2}{2m}\vec{\nabla}^2 + v_{\text{ext},s}(\vec r)$};
  \node [box,below=0.5 of hamiltonian] (se) {$\hat{H}_{KS} \phi_i(\vec r)= E_i \phi_i(\vec r)$};
  \node [box,below=0.5 of se] (density) {$\rho(\vec r)=\sum_{i=1}^n f_i\,|\phi_i(\vec r_i)|^2$};
  \node [box,below=0.5 of density] (criterion) {Convergence criterion satisfied?};

  \path
  (potential.north west) ++(-1em,1em) coordinate (potential fit)
  (criterion.south east) ++(1em,-1em) coordinate (criterion fit);

  \node [box,above=1.5 of potential, fill=orange!30, text width=20em] (initial) {Supply initial density guess $\rho_\text{ini}(\vec r)$ to Kohn Sham equations};
  \node [box,below=1.5 of criterion, fill=blue!30, text width=20em] (energy) {Use $\rho_\text{fin}(\vec r)$ to minimize total energy functional $E_{V_\text{ext}}[\rho]=T_{e,s}[\phi_i\{\rho\}] + V_{ee,H}[\rho] + E_{xc}[\rho] + V_{eI}[\rho]$};

  \path [arrow] (initial) -- (potential);
  \path [arrow] (potential) -- (hamiltonian);
  \path [arrow] (hamiltonian) -- (se);
  \path [arrow] (se) -- (density);
  \path [arrow] (density) -- (criterion);

  \node [rectangle,draw,dashed,inner sep=1em,fit=(potential fit) (criterion fit)] (enclosure) {};
  \node [above=-0.8em of enclosure,anchor=south,draw,outer sep=0pt,fill=white] (enclosure label) {\Large\textbf{Kohn-Sham method}};

  \path [arrow] (criterion) -- (energy) node [midway,left=0.1,draw,outer sep=0pt,fill=white] (TextNode) {Yes};
  \path [draw,thick] (criterion.south) ++(0em,-1em) -- (criterion fit) node [midway,below=0.1,sloped,draw,outer sep=0pt,fill=white] (TextNode) {No};
  \draw [arrow] (criterion fit) |- (potential.east);

\end{tikzpicture}
\end{document}