« home

Kohn-Sham DFT User Choices

Tags

physicsquantum-mechanicsdensity-functional-theoryKohn-Sham

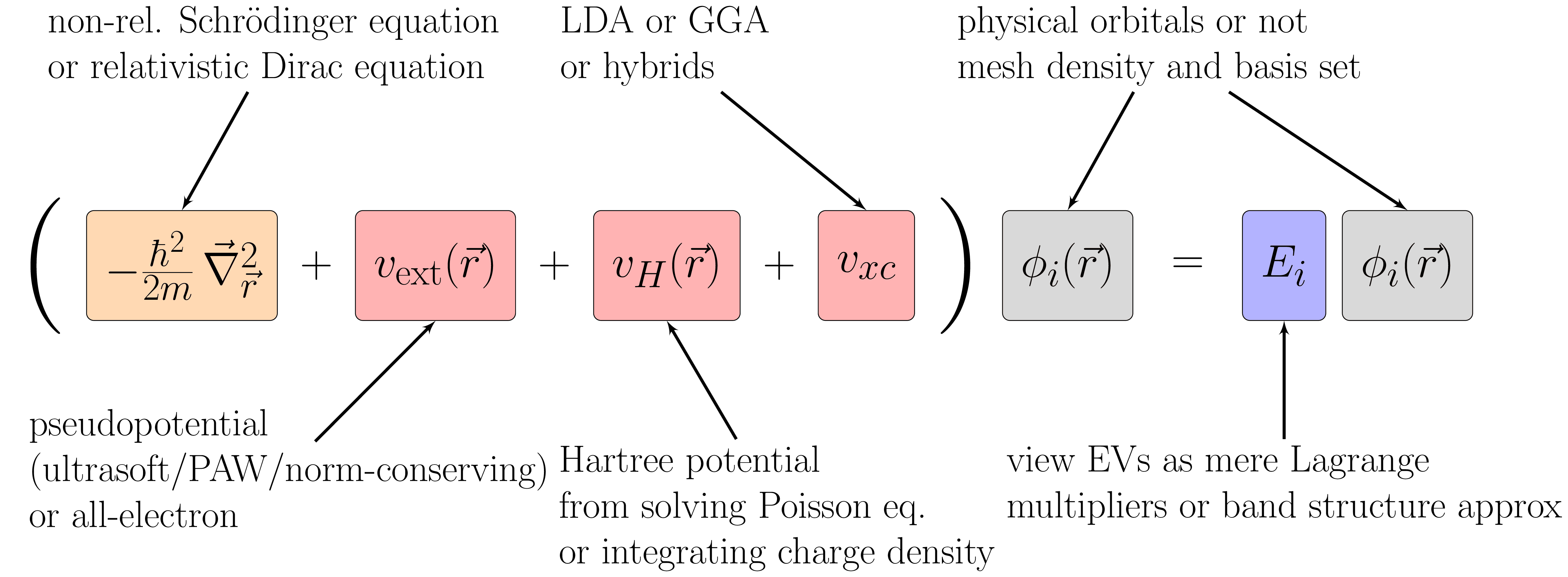
Visualization of the many choices involved in a Kohn-Sham calculation. It can be non-relativistic based on the classical Schrödinger equation or fully relativistic based on the Dirac equation which includes spin-orbit coupling. The near-core electrons can be modeled explicitly in an all-electron calculation or, much more commonly, incorporated along with the nucleus into an effective pseudo-potential. The Hartree energy can be obtained by integrating the charge density or by solving the Poisson equation. The exchange-correlation potential can be treated with a huge library of density functionals, most commonly LDA and GGA. The wave functions can be computed on a numerical mesh and expanded in one of many possible basis sets, e.g. plane waves, APW, or PAW. Inspired by fig. 3 in arxiv:cond-mat/0211443.


Kohn-Sham DFT User Choices

  Edit

Overleaf Logo Open in Overleaf

  Download

PNG PNG (HD) PDF SVG TeX

  Code

dft-choices.tex (44 lines)

\documentclass[tikz]{standalone}

\usetikzlibrary{positioning,arrows}

\begin{document}
\begin{tikzpicture}[
    g/.style={rectangle,draw,rounded corners,minimum height=6em,inner sep=1em,font=\Huge},
    w/.style={font=\Huge},
    c/.style={node distance=15ex,align=left,font=\huge},
    arrow/.style={draw,-latex',ultra thick}
  ]

  \node [w,scale=3] (bra) {(};
  \node [node distance=0ex,fill=orange!30,g,right=of bra] (kinetic) {$-\frac{\hbar^2}{2m}\,\vec{\nabla}_{\vec{r}}^2$};
  \node [node distance=2ex,w,right=of kinetic] (plus1) {$+$};
  \node [node distance=2ex,fill=red!30,g,right=of plus1] (external) {$v_\mathrm{ext}(\vec{r})$};
  \node [node distance=2ex,w,right=of external] (plus2) {$+$};
  \node [node distance=2ex,fill=red!30,g,right=of plus2] (hartree) {$v_H(\vec{r})$};
  \node [node distance=2ex,w,right=of hartree] (plus3) {$+$};
  \node [node distance=2ex,fill=red!30,g,right=of plus3] (xc) {$v_{xc}$};
  \node [node distance=0ex,w,right=of xc,scale=3] (ket) {)};
  \node [node distance=0ex,fill=gray!30,g,right=of ket] (phi1) {$\phi_i(\vec{r})$};
  \node [node distance=4ex,w,right=of phi1] (equal) {$=$};
  \node [node distance=4ex,fill=blue!30,g,right=of equal] (energy) {$E_i$};
  \node [node distance=2ex,fill=gray!30,g,right=of energy] (phi2) {$\phi_i(\vec{r})$};

  \node [c,above=of kinetic,xshift=5em] (kinetic comment) {non-rel. Schrödinger equation\\or relativistic Dirac equation};
  \node [c,below=of external,xshift=-8em,yshift=2em] (external comment) {pseudopotential\\(ultrasoft/PAW/norm-conserving)\\or all-electron};
  \node [c,below=of hartree,xshift=6em] (hartree comment) {Hartree potential\\from solving Poisson eq.\\or integrating charge density};
  \node [c,above=of xc,xshift=-11em] (xc comment) {LDA or GGA\\or hybrids};
  \node [c,above=of phi1,xshift=5em] (phi comment) {physical orbitals or not\\mesh density and basis set};
  \node [c,below=of energy] (energy comment) {view EVs as mere Lagrange\\multipliers or band structure approx};

  \path [arrow] (kinetic comment) -- (kinetic.north);
  \path [arrow,shorten <=-3em] (external comment) -- (external.south);
  \path [arrow] (hartree comment) -- (hartree.south);
  \path [arrow] (xc comment) -- (xc.north);
  \path [arrow] (phi comment) -- (phi1.north);
  \path [arrow] (phi comment) -- (phi2.north);
  \path [arrow] (energy comment) -- (energy.south);

\end{tikzpicture}
\end{document}