« home

Closed String Topologies

Tags

physicsstring theory

When calculating scattering amplitudes via the path integral, we must sum over all possible world-sheet topologies. To characterize the types of world-sheets that have to be considered at each level of its perturbative expansion, string theory makes use of the following theorem:

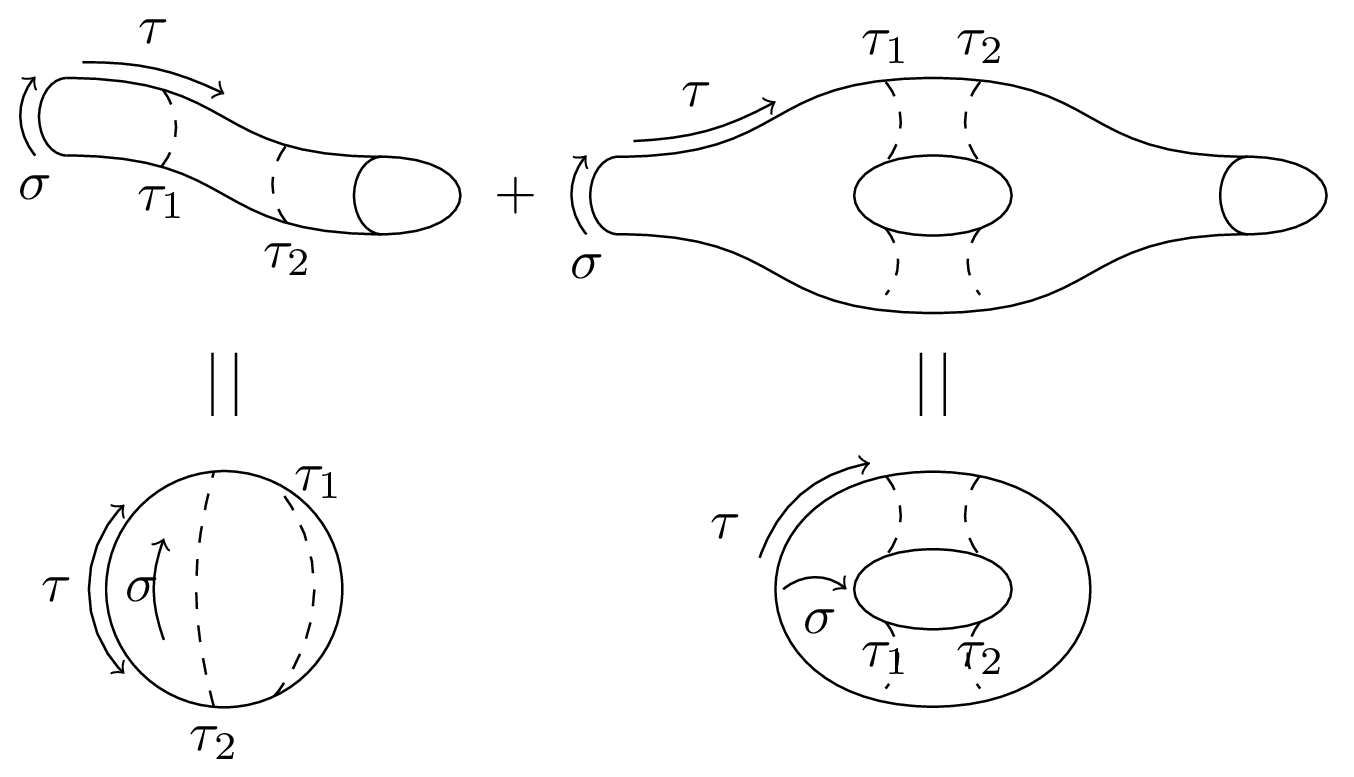
Every compact, connected, oriented two-dimensional manifold is topologically equivalent to a sphere with gg handles (gg for genus) and bb boundaries. A topological invariant of two-dimensional oriented surfaces is the Euler characteristic χ=2−2g−b\chi = 2 - 2g - b.

What this boils down to is that we can obtain the topological characteristics of higher and higher loop-level world-sheet topologies by successively increasing in one-step increments the number of handles gg in case of the closed string and the number of boundaries bb for the open sector. This gives the topologies in this figure for the vacuum diagram of the closed sector up to one-loop level. For the open sector, see open string topologies.


Closed String Topologies

  Edit

Overleaf Logo Open in Overleaf

  Download

PNG PNG (HD) PDF SVG TeX

  Code

closed-string-topologies.tex (114 lines)

\documentclass[tikz]{standalone}

\usetikzlibrary{tqft,calc}

\begin{document}

\begin{tikzpicture}[
    every tqft/.append style={
        transform shape, rotate=90, tqft/circle x radius=7pt,
        tqft/boundary separation=1cm, tqft/view from=incoming
      }
  ]

  % cobordism at upper left
  \pic[
    tqft/cylinder to prior,
    name=a,
    every incoming lower boundary component/.style={draw},
    every outgoing lower boundary component/.style={draw},
    cobordism edge/.style={draw},
  ];
  \pic[
    tqft/cup,
    cobordism edge/.style={draw},
    at=(a-outgoing boundary),
  ];

  % annotation of cobordism at upper left
  \coordinate (temp1) at ($(a-incoming boundary.west)!0.3!(a-outgoing boundary.west) +(0,0.08)$);
  \coordinate (temp2) at ($(a-incoming boundary.west)!0.7!(a-outgoing boundary.west) +(0,-0.08)$);
  \draw[dashed]
  (temp1) node[below] {$\tau_1$} to[bend right=40] ++(0,0.5)
  (temp2) node[below] {$\tau_2$} to[bend left=40] ++(0,0.5);
  \draw[->] ($(a-incoming boundary.west) - (0.2,0)$) node[below] {$\sigma$} to[bend left=40] ++(0,0.5);
  \draw (a-outgoing boundary) ++(0.85,0) node {$+$};
  \draw[->] ($(a-incoming boundary.east)+(0.1,0.1)$) to[bend left=13] +(0.9,-0.2);
  \node[above] at ($(a-incoming boundary.east)+(0.55,0.1)$) {$\tau$};

  % cobordism at upper right consisting of two 'pants' and a cup
  \pic[
    tqft/pair of pants,
    name=b,
    every incoming lower boundary component/.style={draw},
    cobordism edge/.style={draw},
    at={($(a-outgoing boundary)+(1.5,0)$)},
  ];
  \pic[
    tqft/reverse pair of pants,
    name=c,
    every outgoing lower boundary component/.style={draw},
    cobordism edge/.style={draw},
    at=(b-outgoing boundary 1),
  ];
  \pic[
    tqft/cup,
    cobordism edge/.style={draw},
    at=(c-outgoing boundary),
  ];

  % annotation of cobordism at upper right
  \draw[->] ($(b-incoming boundary.west) - (0.2,0)$) node[below] {$\sigma$} to[bend left=40] ++(0,0.5);
  \coordinate (temp1) at ($(b-between outgoing 1 and 2)!0.2!(c-between incoming 1 and 2) +(0,0.72)$);
  \coordinate (temp2) at ($(b-between outgoing 1 and 2)!0.8!(c-between incoming 1 and 2) +(0,0.72)$);
  \draw[dashed]
  (temp1) node[above] {$\tau_1$} to[bend left=40] +(0,-0.51) ++(0,-0.93) to[bend left=40] ++(0,-0.42)
  (temp2) node[above] {$\tau_2$} to[bend right=40] +(0,-0.51) ++(0,-0.93) to[bend right=40] ++(0,-0.42);
  \draw[->] ($(b-incoming boundary.east)+(0.1,0.1)$) to[bend right=13] +(0.9,0.25);
  \node[above] at ($(b-incoming boundary.east)+(0.5,0.2)$) {$\tau$};

  % drawing ring
  \pic[
    tqft ,
    name=d,
    incoming boundary components=0,
    outgoing boundary components=2,
    cobordism edge/.style={draw},
    anchor=between outgoing 1 and 2,
    at={($(b-between outgoing 1 and 2)!0!(c-between incoming 1 and 2) - (0,2.5)$)},
  ];

  \pic[
    tqft ,
    name=e,
    incoming boundary components=2,
    outgoing boundary components=0,
    cobordism edge/.style={draw},
    at = {(d-outgoing boundary 1)},
  ];
  \coordinate (temp1) at ($(d-between outgoing 1 and 2)!0.2!(e-between incoming 1 and 2) +(0,0.72)$);
  \coordinate (temp2) at ($(d-between outgoing 1 and 2)!0.8!(e-between incoming 1 and 2) +(0,0.72)$);
  \draw[dashed]
  (temp1) to[bend left=40] +(0,-0.51) ++(0,-0.93) node[below] {$\tau_1$} to[bend left=40] ++(0,-0.42)
  (temp2) to[bend right=40] +(0,-0.51) ++(0,-0.93) node[below] {$\tau_2$} to[bend right=40] ++(0,-0.42);

  \coordinate (temp1) at ($(d-between outgoing 1 and 2)!0.5!(e-between incoming 1 and 2)$);
  \coordinate (temp2) at (a-between first incoming and first outgoing);
  \draw[->] ($(e-incoming boundary 2)+(-1.1,-0.3)$) node[above left] {$\tau$} to[bend left=30] +(0.7,0.6);
  \draw [->] ($(d-between outgoing 1 and 2) + (-0.45,0)$) node [below right] {$\sigma$} to[bend left=40] +(0.4,0);
  \draw (temp1) ++(-0.075,1.5) -- ++(0,-0.4) ++(0.15,0) -- +(0,0.4);

  % drawing and annotating ball
  \node[draw, shape=circle, minimum width=1.5cm]
  at (temp1-|temp2) (circ) {};
  \draw[dashed] (circ) +(265:0.75) node[below] {$\tau_2$} to[bend left=15] +(95:0.75);
  \draw[dashed] (circ) +(295:0.75) to[bend right=40] +(65:0.75) node[right] {$\tau_1$};
  \draw[->] (circ) +(220:0.5) to[bend left=20] +(140:0.5);
  \node[right] at(circ.west) {$\sigma$};
  \draw (circ) ++(-0.075,1.5) -- ++(0,-0.4) ++(0.15,0) -- +(0,0.4);
  \draw[<->] (circ.south west) +(-0.1,0) to[bend left=45] ($(circ.north west)+(-0.1,0)$);
  \node[left=0.25em] at(circ.west) {$\tau$};
\end{tikzpicture}

\end{document}