« home

Wyckoff Positions

(original)

Tags

physicssolid state physicssymmetriesgroup theory

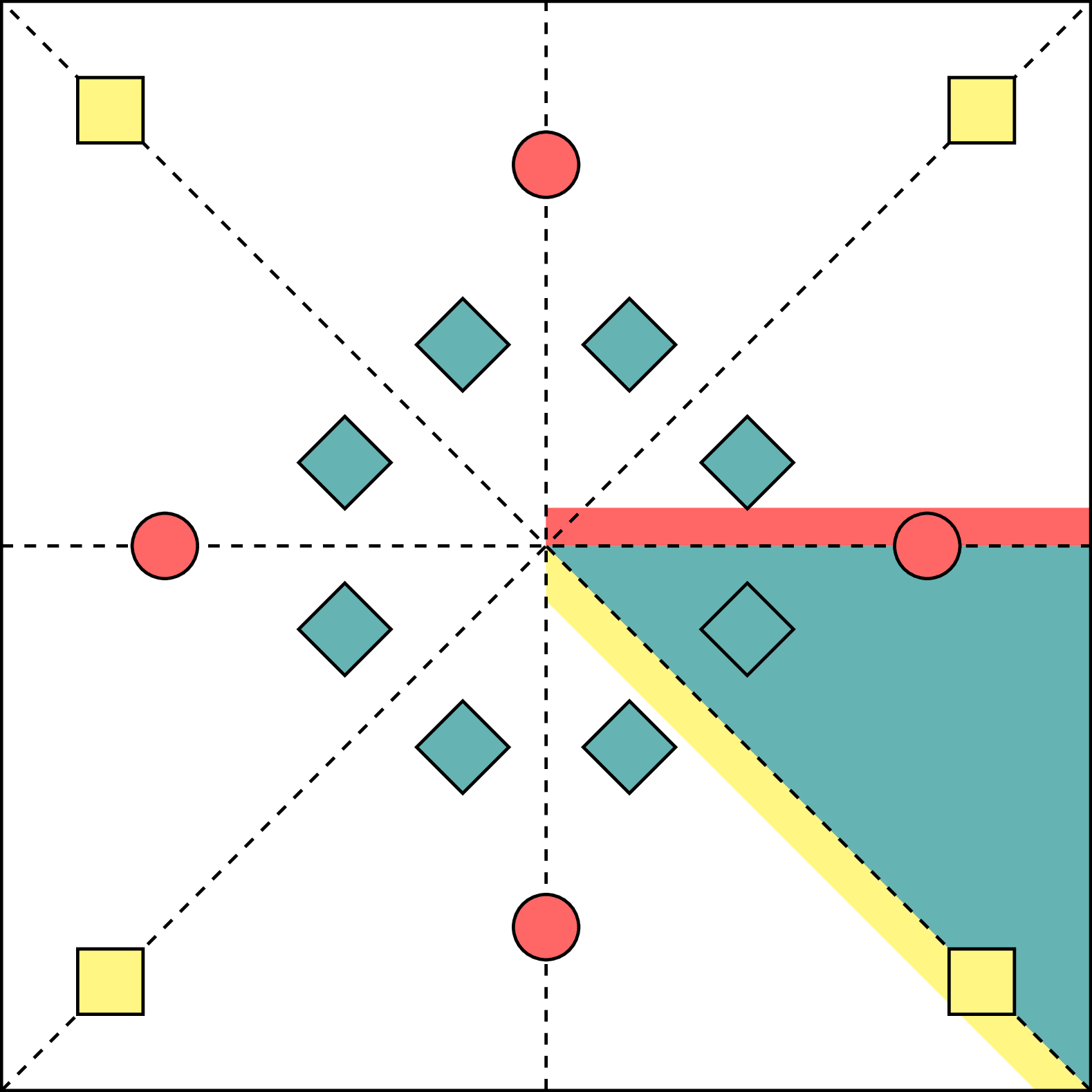
2D toy crystal with three occupied Wyckoff positions. The shaded areas illustrate the region of the unit cell the relevant atoms are constrained to lie in by specifying an anonymized Wyckoff position for that atom. Reproduction of fig. 2 from "Wyckoff Set Regression for Materials Discovery" by Rhys Goodall, inspired by PyXtal docs.


Wyckoff Positions

  Edit

Overleaf Logo Open in Overleaf

  Download

PNG PNG (HD) PDF SVG TeX

  Code

wyckoff-positions.tex (25 lines)

\documentclass[tikz]{standalone}

\begin{document}
\begin{tikzpicture}[thick]
  \def\r{5}
  \fill[teal!60] (\r,-\r) -- (0,0) -- (\r,0) -- cycle;
  \fill[yellow!60] (\r,-\r) -- (0,0) -- (0,-0.\r) -- (4.\r,-\r) -- cycle;
  \fill[red!60] (0,0) rectangle (\r,0.3\r);
  \draw (-\r,-\r) rectangle (\r,\r);
  \draw[dashed] (-\r,-\r) -- (\r,\r) (\r,-\r) -- (-\r,\r) (-\r,0) -- (\r,0) (0,-\r) -- (0,\r);

  \foreach \a in {-0.8*\r,0.8*\r}
  \foreach \b in {-0.8*\r,0.8*\r}
  \draw[fill=yellow!60] (\a,\b) +(-0.3,-0.3) rectangle +(0.3,0.3);

  \foreach \a in {-0.7*\r,0.7*\r} {
      \draw[fill=red!60] (\a,0) circle (0.3);
      \draw[fill=red!60] (0,\a) circle (0.3);
    }

  \foreach \i in {1,...,8}
  \draw[rotate=45,fill=teal!60] (\i*360/8+22.5:2cm) +(-0.3,-0.3) rectangle +(0.3,0.3);
\end{tikzpicture}
\end{document}