Thermodynamic Ensemble transforms
Tags
Equivalence of thermodynamic ensembles through Laplace and Legendre transforms.
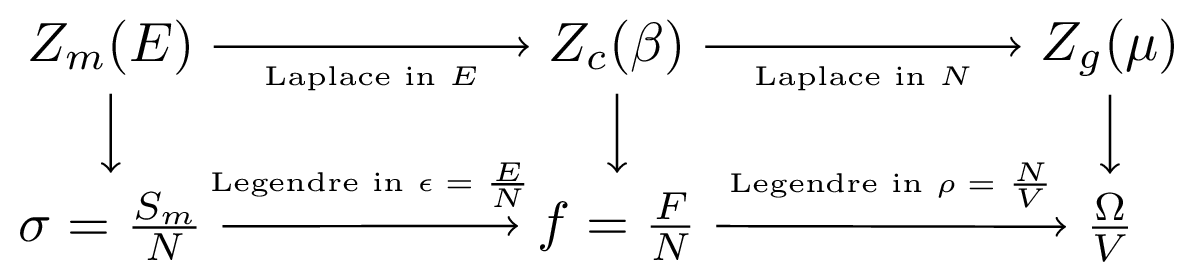
Edit
Download
Code
thermo-ensemble-trafos.tex (30 lines)
\documentclass[tikz]{standalone}
\usetikzlibrary{positioning}
\begin{document}
\begin{tikzpicture}[trafo/.style={midway,font=\tiny}]
\def\hd{2}\def\vd{0.5}
\node (Zm) at (0,0) {$Z_m(E)$};
\node[right=\hd of Zm] (Zc) {$Z_c(\beta)$};
\node[right=\hd of Zc] (Zg) {$Z_g(\mu)$};
\node[below=\vd of Zm] (Sm) {$\sigma = \frac{S_m}{N}$};
\node[below=\vd of Zc] (F) {$f = \frac{F}{N}$};
\node[below=\vd of Zg] (O) {$\frac{\Omega}{V}$};
\draw[->] (Zm) -- (Sm);
\draw[->] (Zc) -- (F);
\draw[->] (Zg) -- (O);
\draw[->] (Zm) -- (Zc) node[trafo,below] {Laplace in $E$};
\draw[->] (Zc) -- (Zg) node[trafo,below] {Laplace in $N$};
\draw[->] (Sm) -- (F) node[trafo,above] {Legendre in $\epsilon = \frac{E}{N}$};
\draw[->] (F) -- (O) node[trafo,above] {Legendre in $\rho = \frac{N}{V}$};
\end{tikzpicture}
\end{document}