M-Theory
Tags
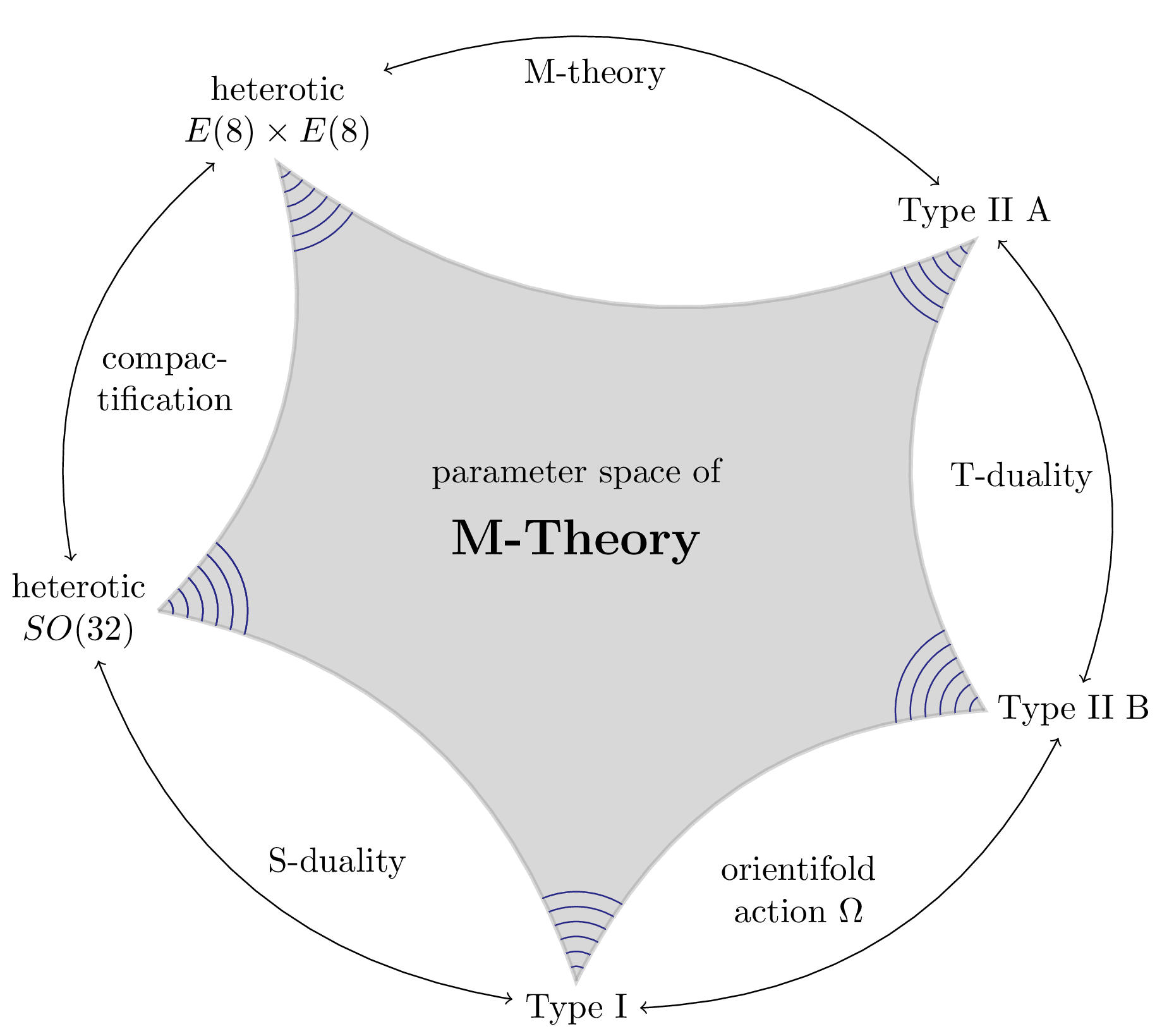
One of the pivotal insights of the 2nd superstring revolution point was Edward Witten's formulation of M-Theory in 1995. Before that, there had been 5 different types of string theories, each 10-dimensional: Type I, Type IIa and IIb, and two different heterotic theories. Witten showed that all of these theories are simply different limiting cases of a single overarching string theory (without showing what that underlying theory actually is). See Sean Carroll's excellent post on M-Theory for details.
Edit
Download
Code
m-theory.tex (41 lines)
\documentclass[tikz,svgnames]{standalone}
\begin{document}
\begin{tikzpicture}
\node (so32) [align=center] at (-5,-1) {heterotic\\$SO(32)$};
\node (e8e8) [align=center] at (-3,4) {heterotic\\$E(8) \times E(8)$};
\node (tiia) [align=center] at (4,3) {Type II A};
\node (tiib) [align=center] at (5,-2) {Type II B};
\node (ti) [align=center] at (0,-5) {Type I};
\draw[bend left,<->] (so32) to node [below right,align=center] {compac-\\tification} (e8e8);
\draw[bend left,<->] (e8e8) to node [below left] {M-theory} (tiia);
\draw[bend left,<->] (tiia) to node [below left] {T-duality} (tiib);
\draw[bend left,<->] (tiib) to node [above left,align=center] {orientifold\\action $\Omega$} (ti);
\draw[bend left,<->] (ti) to node [above right] {S-duality} (so32);
\begin{scope}
\clip[bend right]
(so32.east)
to (e8e8.south)
to (tiia.south)
to (tiib.west)
to (ti.north)
to (so32.east);
\foreach \c in {so32.east,e8e8.south,tiia.south,tiib.west,ti.north,so32.east}{%
\foreach \r in {1,...,6}{%
\draw[DarkBlue] (\c) circle (\r*0.15cm);
}
}
\end{scope}
\draw[bend right,very thick,gray,fill,fill opacity=0.3] (so32.east) to (e8e8.south) to (tiia.south) to (tiib.west) to (ti.north) to (so32.east);
\node (mth) [align=center] at (0,0) {parameter space of\\[2ex]{\Large \textbf{M-Theory}}};
\end{tikzpicture}
\end{document}