Identical Particle Energy Distribution Function Comparison

Tags

physicsstatistical-mechanicsBose-EinsteinBoltzmannFermi-Diracpgfplots

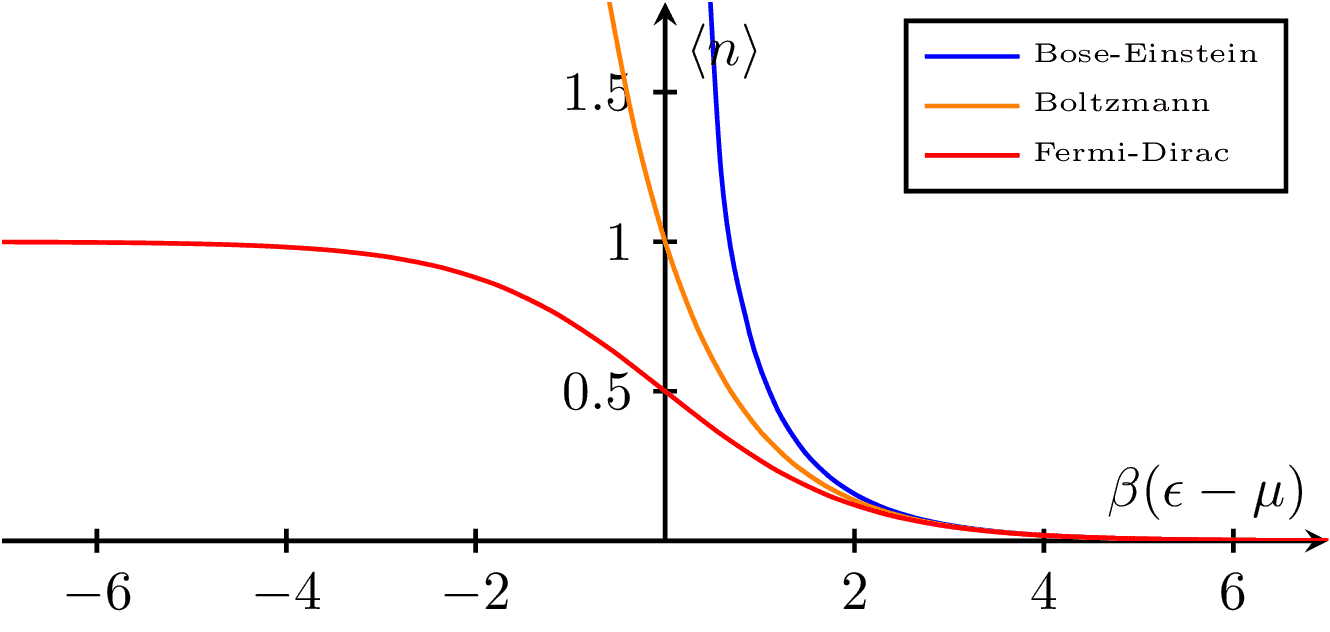
A plot comparing the distribution functions of Bose-Einstein, Boltzmann, and Fermi-Dirac statistics as a function of the reduced chemical potential $\beta (\epsilon - \mu)$ . This visualization highlights the differences between the three types of distribution functions, which are used to describe the behavior of particles in different statistical systems.

Identical Particle Energy Distribution Function Comparison

Edit

Open in Overleaf

Download

PNG PNG (HD) PDF SVG TeX

Code

energy-distribution-functions.tex (29 lines)

\documentclass{standalone}

\usepackage{pgfplots}
\pgfplotsset{compat=newest}

\begin{document}
\begin{tikzpicture}
  \begin{axis}[
      xlabel = $\beta (\epsilon - \mu)$,
      ylabel = $\langle n\rangle$,
      ymin = 0,ymax = 1.8,
      smooth,thick,
      axis lines = center,
      every tick/.style = {thick},
      legend cell align=left,
      legend style={legend pos=north east,font=\tiny},
      width=10cm,height=5cm]

    \def\xmax{7}
    \addplot[color=blue,domain=0:\xmax]{1/(e^x - 1)};
    \addplot[color=orange,domain=-1:\xmax]{1/e^x};
    \addplot[color=red,domain = -\xmax:\xmax]{1/(e^x + 1)};

    \legend{Bose-Einstein,Boltzmann,Fermi-Dirac}

  \end{axis}
\end{tikzpicture}
\end{document}