« home

Cylinder to Plane

Tags

physicsstring theorytopology

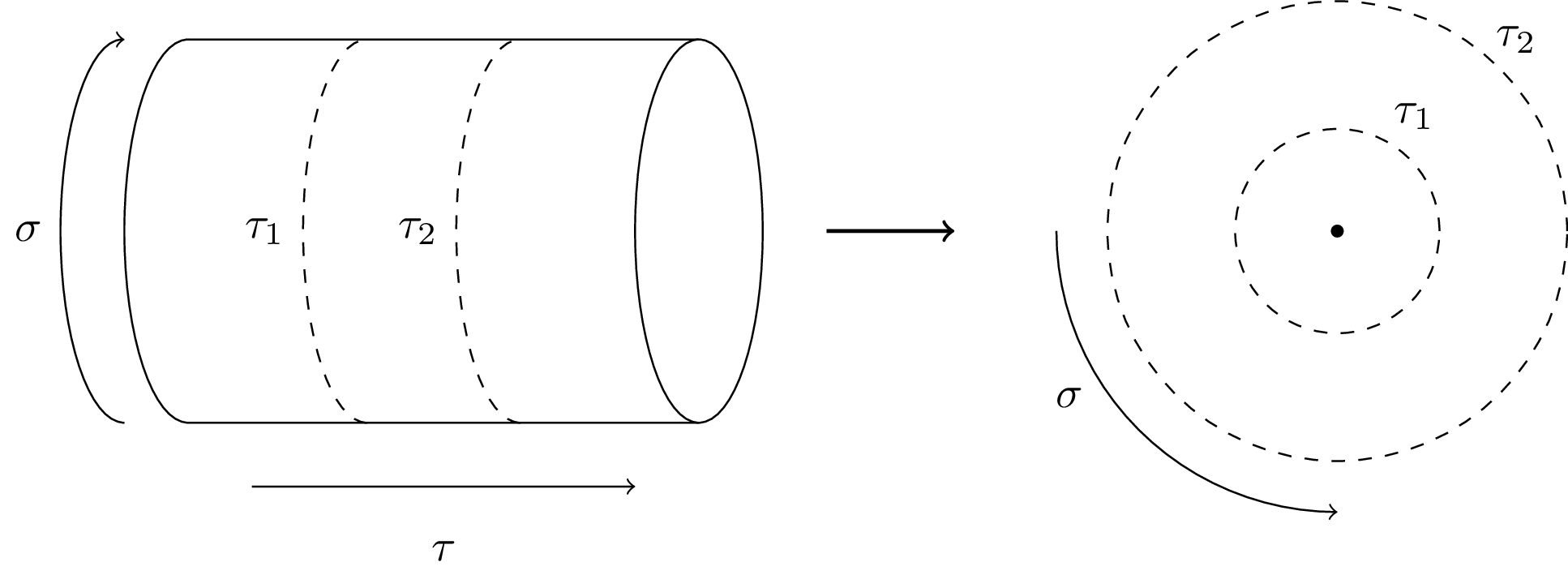
String theory: Primary fields and radial quantization A time-ordered product of fields on the cylinder maps to a radially ordered product in the complex plane. This graphic visualizes how different times on the cylinder correspond to different times on the plane.


Cylinder to Plane

  Edit

Overleaf Logo Open in Overleaf

  Download

PNG PNG (HD) PDF SVG TeX

  Code

cylinder-to-plane.tex (31 lines)

\documentclass[tikz]{standalone}

\begin{document}
\begin{tikzpicture}

  \draw[dashed] (2.6,0) arc (-90:90:-0.5 and 1.5);% line 1
  \draw[dashed] (1.4,0) arc (-90:90:-0.5 and 1.5);% line 2
  \draw[->] (-0.5,0) arc (-90:90:-0.5 and 1.5);
  \draw (0,0) -- (4,0);% bottom line
  \draw (0,3) -- (4,3);% top line
  \draw (0,0) arc (270:90:0.5 and 1.5);% left half of the left ellipse
  \draw (4,1.5) ellipse (0.5 and 1.5);% right ellipse
  \draw (0.6,1.5) node {$\tau_1$};
  \draw (1.8,1.5) node {$\tau_2$};
  \draw (-1.25,1.5) node {$\sigma$};
  \draw[->] (0.5,-0.5) -- (3.5,-0.5);
  \draw (2,-1) node {$\tau$};

  \draw[->,thick] (5.0,1.5) -- (6,1.5);

  \draw[dashed] (9,1.5) circle (0.8);
  \draw[dashed] (9,1.5) circle (1.8);
  \draw [->,domain=0:90] plot ({9 - 2.2*cos(\x)},{1.5-2.2*sin(\x)});
  \draw (6.9,0.2) node {$\sigma$};
  \draw (9.6,2.4) node {$\tau_1$};
  \draw (10.4,3) node {$\tau_2$};
  \node at (9,1.5) [circle,inner sep=1pt,fill=black] {};

\end{tikzpicture}
\end{document}