Temperature-Dependent Phase Transition

Tags

physicsthermodynamicsphase-transitionstemperaturecritical-temperaturepgfplots

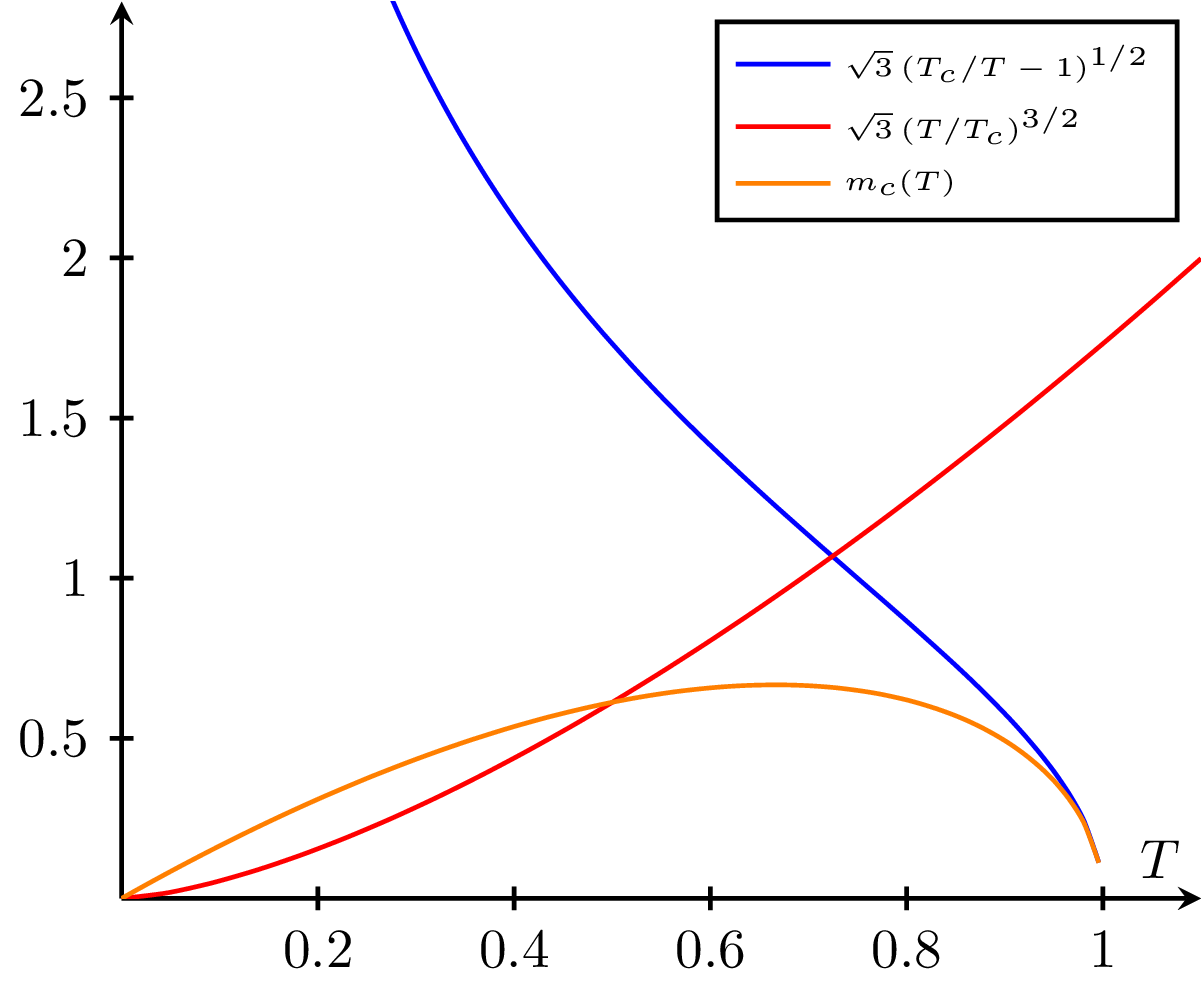
A plot illustrating the temperature-dependent phase transitions of a material as a function of the critical temperature ( $T_c$ ). The blue curve represents the low-temperature phase, the red curve represents the high-temperature phase, and the orange curve shows the critical mass ( $m_c$ ) as a function of temperature. This visualization helps to understand the behavior of materials as they undergo phase transitions due to changes in temperature.

Edit

Open in Overleaf

Download

PNG PNG (HD) PDF SVG TeX

Code

critical-temperature.tex (30 lines)

\documentclass{standalone}

\usepackage{pgfplots}
\pgfplotsset{compat=newest}

\begin{document}
\begin{tikzpicture}
  \begin{axis}[
      xlabel = $T$,
      smooth,thick,
      domain=0:1.1,
      ymax=2.8,
      axis lines = center,
      every tick/.style = {thick},
      legend cell align=left,
      legend style={font=\tiny}]

    \def\Tc{1}
    \addplot[color=blue,samples=75]{sqrt(3)*(\Tc/x - 1)^(1/2)};
    \addplot[color=red]{sqrt(3)*(x/\Tc)^(3/2)};
    \addplot[color=orange,samples=75]{sqrt(3)*(x/\Tc)^(3/2)*(\Tc/x - 1)^(1/2)};

    \legend{$\sqrt{3} \left(T_c/T - 1\right)^{1/2}$,
      $\sqrt{3} \left(T/T_c\right)^{3/2}$,
      $m_c(T)$}

  \end{axis}
\end{tikzpicture}
\end{document}