« home

Convex Functions

Tags

math

xx and −xlog⁡(x)-x\log(x) are concave functions. Since ln⁡(p)\ln(p) decomposes into sums of these two components, it too must be concave. Any extremum of a concave function is a maximum. This fact is used in statistical physics to find the equilibrium distribution of many-particle systems. See problem 2 on this exercise sheet.


Convex Functions

  Edit

Overleaf Logo Open in Overleaf

  Download

PNG PNG (HD) PDF SVG TeX

  Code

convex-functions.tex (26 lines)

\documentclass{standalone}

\usepackage{pgfplots}
\pgfplotsset{compat=newest}

\begin{document}
\begin{tikzpicture}
  \begin{axis}[
      domain=0:2.7,
      xlabel=$x$,
      smooth,thick,
      axis lines=center,
      every tick/.style={thick},
      legend style={cells={anchor=west}},
      legend pos=north west]

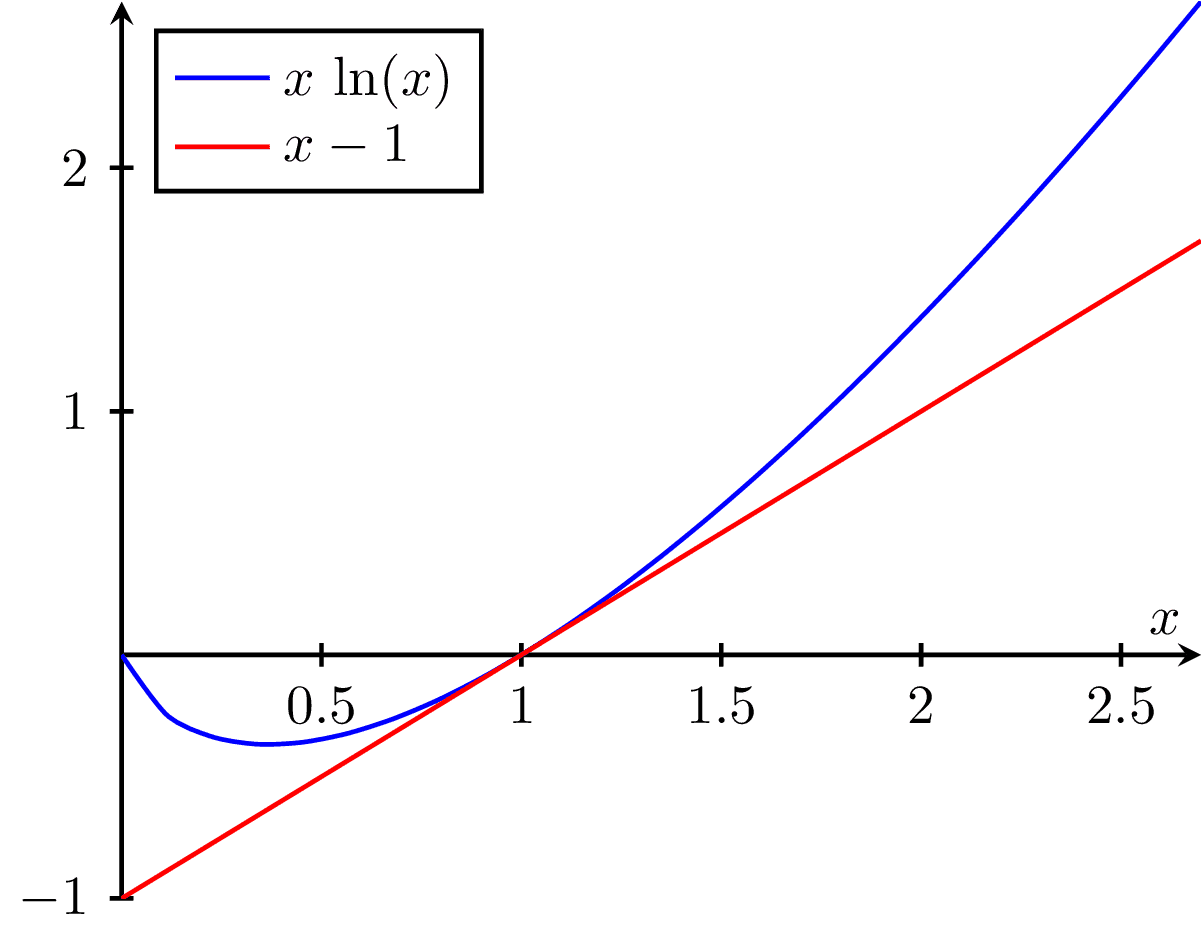
    \addplot[color=blue]{x*ln(x)};

    \addplot[color=red]{x-1};

    \legend{$x \, \ln(x)$,$x-1$}

  \end{axis}
\end{tikzpicture}
\end{document}